Formation Python
Lycée Saint-Denis - Annonay
Atelier Variables Aléatoires

Retour

Librairie utilisée

Pour simuler des variables aléatoires, nous utiliserons la librairie numpy intégrée à Python afin de générer des nombres "aléatoires".

from numpy.random import *
random() # Retour un nombre appartenant à [0, 1[
randint(a, b) # Retourne un entier appartenant à [[a, b[[

Cela permet déjà dans un premier temps de simuler une loi uniforme.

Loi de Bernoulli

Créer une fonction bernoulli qui prendra en argument le paramètre p afin de simuler la loi de Bernoulli.

from numpy.random import *

def bernoulli(p):
	if random() < p:
		return 1
	else:
		return 0

from numpy.random import *

def bernoulli(p):
	return 1*(random() < p)

Loi Binomiale

Créer une fonction binomiale qui prendra en argument les paramètres n et p afin de simuler la loi Binomiale.

from numpy.random import *

# Première version en utilisant la fonction bernoulli précédente
def binomiale(n, p):
	s = 0
	for k in range(n):
		s += bernoulli(p)
	return s

################################################################

# Deuxième version (sans pré-requis)
def binomiale(n, p):
    i = 0
    for i in range(n):
        if random() < p:
            i += 1
    return i

Moyenne d'un lancé de dé

Créer une fonction histogramme qui prendra en argument deux entiers N qui va simuler N lancés de dés et qui retourne un histogramme des valeurs prises.

Que peut-on constater ?

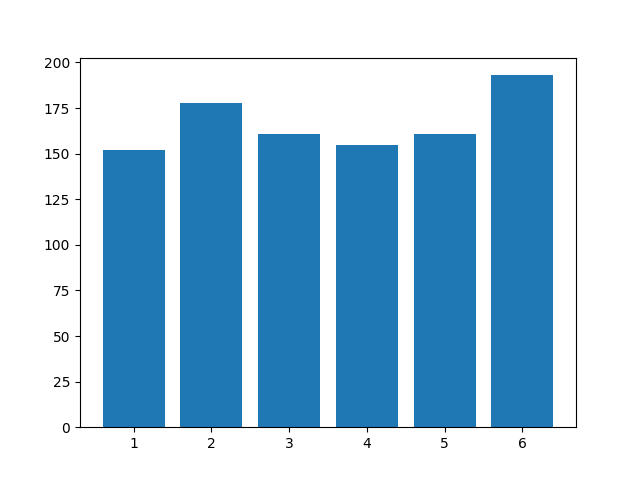
from matplotlib.pyplot import *

hist(valeurs, rwidth=0.8, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5])
# permet d'afficher les valeurs sur les intervalles [0.5, 1.5], [1.5, 2.5], ...

Moyenne / Espérance

Créer une fonction moyenne qui prendra en argument deux entiers N et p qui va simuler N variables aléatoires suivant une loi de Bernoulli de paramètre p et qui retourne la moyenne empirique de tous les résultats.

Cette valeur tend vers l'espérance de la variable aléatoire quand N tend vers l'infini (c'est la loi des grands nombres).

Exercice 1 (le juste prix)

L’ordinateur choisit au hasard un nombre entier compris entre 1 et 25.
Le joueur ne le connaît pas et doit le deviner en un minimum d’essais.

Jeu 1 : Quand le joueur propose un nombre, l'ordi ne peut répondre que par ''Oui'' ou ''Non''.
Le jeu s'arrête lorsque le joueur a trouvé le nombre mystère ; on affiche alors le nombre d'essais.
Jeu 2 : Quand le joueur propose un nombre, l'ordi répondra ''Plus'' ou ''Moins''.
On peut alors faire moins de proposition et gagner plus rapidement.

Exercice 2 (marche aléatoire)

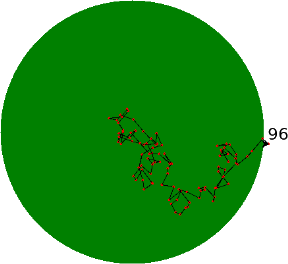
On trace un disque de rayon 100 pixels. On commence au centre.
On se déplace successivement d’un nombre de pixels aléatoire entre −20 et 20 horizontalement, et aussi verticalement.
Si on sort du disque, on s’arrête et on affiche le nombre d’étapes effectuées.

Utiliser la librairie turtle pour tracer des courbes.

from turtle import *

dot(100, 'green') # permet de tracer un point / cercle de 50 de diamètre en couleur verte

goto(x, y) # permet de déplacer le curseur aux coordonnées (x, y)

write(valeur) # permet d'afficher la variable valeur

done() # OBLIGATOIRE à la fin du fichier pour stopper le graphique

TP Lycée

Voici un exemple de TP à proposer à vos élèves pour étudier le comportement d'une marche aléatoire.

Cliquer ici pour y accéder

Loi Géométrique

Créer une fonction geometrique qui prendra en argument le paramètre p afin de simuler la loi Géométrique.

def geometrique(p):
	s = 0
	k = 0
	while s == 0:
		s = bernoulli(p)
		k += 1
	return k

Comme précédemment, tester un grand nombre de simulations et calculer la moyenne.

N = 10000
p = 0.5
s = 0
for k in range(N):
	s += geometrique(p)
print(s/N)

Librairies

Ces simulations peuvent être effectuées directement avec le même module numpy :

from numpy.random import *

binomial(n, p)
geometric(p)
poisson(mu)

Formation PythonLycée Saint-Denis - Annonay Atelier Variables Aléatoires